A stochastic sampling approach to zircon eruption age interpretation
Affiliations | Corresponding Author | Cite as | Funding informationC.B.K. partially supported by U.S. DOE CSGF under contract DE-FG02-97ER25308.
- Share this article





Article views:6,304Cumulative count of HTML views and PDF downloads.
- Download Citation
- Rights & Permissions
top
Abstract
Figures and Tables
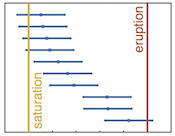
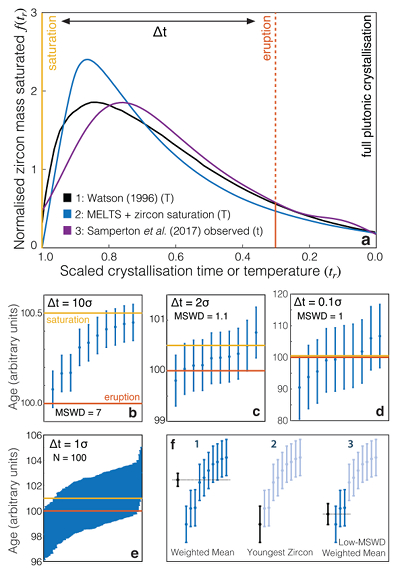 Figure 1 Zircon distributions. (a) Theoretical and empirical relative zircon crystallisation distributions f(tr), scaled from initiation to termination of zircon crystallisation. 1: Kinetic model of Watson (1996), based on zirconium diffusion constraints. 2: Thermodynamic model of Keller et al. (2017) using MELTS calculations. 3: Observed zircon crystallisation distributions of Samperton et al. (2017), shown as a kernel density estimate for all autocrystic zircons, truncated at +/- 1 kernel bandwidth. (b-d) Representative synthetic zircon age datasets for a variety of ∆t/σ at N = 10. (e) Example dataset with N = 100 at ∆t = 1σ; note the range is greater than in c despite lower ∆t. (f) Schematic illustration of the three most common volcanic zircon age interpretations. | 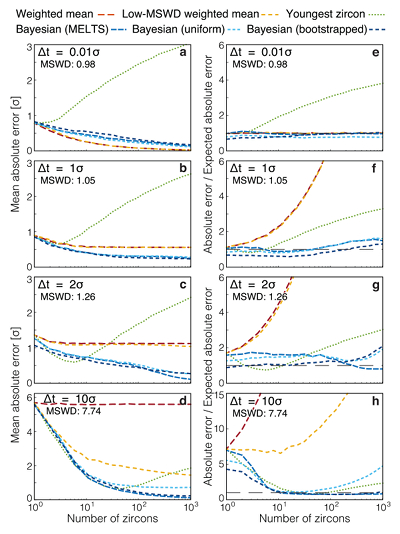 Figure 2 Performance of each age interpretation as a function of N and ∆t/σ. (a-d) Mean absolute error is the mean absolute deviation of the model result from the true value; lower absolute errors are better. (e-h) Accuracy of the model uncertainty for each age interpretation. A value greater than 1.0 indicates an under-estimation of the model uncertainty (i.e. over-precision), while a value lower than 1.0 indicates an over-estimation of the model uncertainty. MSWD in each panel is the average mean square of weighted deviation (also known as the reduced chi squared statistic) for that ∆t/σ over all N. Each datum reflects the mean of 1200 synthetic dataset tests; standard error of the mean is on the order of the line width. | 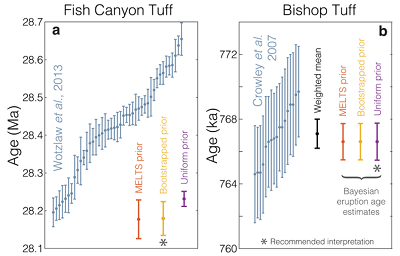 Figure 3 Bayesian eruption age estimates for two well known volcanic zircon populations. For age spectra with well-resolved dispersion (a), a kernel density estimate may recover a close approximation of f(tr), obviating the need to identify and reject antecrysts. However, for age spectra where igneous dispersion is not well resolved (b), assuming a uniform f(tr) may be more parsimonious. |
| Figure 1 | Figure 2 | Figure 3 |
top
Introduction
Absolute time constraints are critical for establishing temporal correlations, testing casual relationships, and quantifying rates and durations throughout the Earth sciences (Reiners et al., 2018
Reiners, P.W., Carlson, R.W., Renne, P.R., Cooper, K.M., Granger, D.E., McLean, N.M., Schoene, B. (2018) Geochronology and Thermochronology. John Wiley & Sons.
). However, the time of radioisotopic closure may not directly date the geological events or processes of interest. Throughout the first century of geochronology, this potential mismatch was frequently a minor concern compared to analytical uncertainties at the percent level or greater. Recently, however, continual improvements in analytical precision and accuracy have fundamentally altered longstanding assumptions of geochronological age interpretation (Schoene, 2014Schoene, B. (2014) 4.10 U–Th–Pb Geochronology. In: Rudnick, R.L. (Ed.) Treatise on Geochemistry, Second Edition. Elsevier, 341–378.
).One chronometer of particular interest is the U-Pb system in zircon, thanks to zircon’s ubiquity, resilience, and tendency to exclude initial daughter isotopes. Throughout the geologic record, zircon provides crucial time constraints for processes ranging from evolution and mass extinction to magmatism and crustal differentiation (Bowring et al., 1993
Bowring, S.A., Grotzinger, J.P., Isachsen, C., Knoll, A., Pelechaty, S., Kolosov, P. (1993) Calibrating rates of early Cambrian evolution. Science 261, 1293–1298.
; Mundil et al., 2004Mundil, R., Ludwig, K.R., Metcalfe, I., Renne, P.R. (2004) Age and Timing of the Permian Mass Extinctions: U/Pb Dating of Closed-System Zircons. Science 305, 1760–1763.
; Harrison, 2009Harrison, T.M. (2009) The Hadean Crust: Evidence from 4 Ga Zircons. Annual Review of Earth and Planetary Sciences 37, 479–505.
; Schoene et al., 2015Schoene, B., Samperton, K.M., Eddy, M.P., Keller, G., Adatte, T., Bowring, S.A., Khadri, S.F.R., Gertsch, B. (2015) U-Pb geochronology of the Deccan Traps and relation to the end-Cretaceous mass extinction. Science 347, 182–184.
; Samperton et al., 2017Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
). Due to extremely slow parent and daughter isotope diffusion (Cherniak, 2003Cherniak, D.J. (2003) Diffusion in Zircon. Reviews in Mineralogy and Geochemistry 53, 113–143.
), zircon U-Pb ages record zircon crystallisation, if not compromised by metamictisation and subsequent Pb loss. However, the crystallisation of a suite of zircons in a single igneous rock sample has often been assumed to occur rapidly relative to analytical uncertainty, justifying the use of statistical approaches such as the weighted mean (e.g., Bowring et al., 1993Bowring, S.A., Grotzinger, J.P., Isachsen, C., Knoll, A., Pelechaty, S., Kolosov, P. (1993) Calibrating rates of early Cambrian evolution. Science 261, 1293–1298.
). Moreover, even though zircon saturation in magmas is empirically well understood and distinct from whole rock crystallisation to the solidus (Boehnke et al., 2013Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
), U-Pb zircon ages are traditionally interpreted within uncertainty as reflecting bulk crystallisation or eruption.While such assumptions may be justified for sufficiently ancient or homogeneous samples, crystallisation timescales may span 200-700 kyr for magmatic zircons (Lissenberg et al., 2009
Lissenberg, C.J., Rioux, M., Shimizu, N., Bowring, S.A., Mével, C. (2009) Zircon Dating of Oceanic Crustal Accretion. Science 323, 1048–1050.
; Wotzlaw et al., 2013Wotzlaw, J.F., Schaltegger, U., Frick, D.A., Dungan, M.A., Gerdes, A., Günther, D. (2013) Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41, 867–870.
; Samperton et al., 2017Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
). Consequently, diachronous crystallisation or recrystallisation must be considered before calculating a weighted mean of zircon ages derived from either in situ (SIMS, LA-ICPMS) or bulk (TIMS) analytical techniques. For instance, modern U-Pb Chemical Abrasion – Isotope Dilution TIMS (CA-ID-TIMS) ages (Mattinson, 2005Mattinson, J.M. (2005) Zircon U–Pb chemical abrasion (“CA-TIMS”) method: Combined annealing and multi-step partial dissolution analysis for improved precision and accuracy of zircon ages. Chemical Geology 220, 47–66.
) on single zircons and zircon fragments may surpass 0.05 % (2σ) accuracy and precision (e.g., Schoene et al., 2015Schoene, B., Samperton, K.M., Eddy, M.P., Keller, G., Adatte, T., Bowring, S.A., Khadri, S.F.R., Gertsch, B. (2015) U-Pb geochronology of the Deccan Traps and relation to the end-Cretaceous mass extinction. Science 347, 182–184.
; Samperton et al., 2017Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
) – equivalent to 50 kyr in a 100 Ma sample. Consequently, zircon crystallisation age heterogeneity is increasingly clearly resolved in a wide range of magmatic contexts (Wotzlaw et al., 2013Wotzlaw, J.F., Schaltegger, U., Frick, D.A., Dungan, M.A., Gerdes, A., Günther, D. (2013) Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41, 867–870.
; Samperton et al., 2017Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
).Analogous issues appear in other geochronological applications ranging from the interpretation of anomalously dispersed Ar-Ar ages (e.g., Ellis et al., 2017
Ellis, B.S., Mark, D.F., Troch, J., Bachmann, O., Guillong, M., Kent, A.J.R., von Quadt, A. (2017) Split-grain 40Ar/39Ar dating: Integrating temporal and geochemical data from crystal cargoes. Chemical Geology 457, 15–23.
) to the estimation of sedimentary depositional ages from detrital mineral geochronology. We consider here the case study of eruption age estimation by CA-ID-TIMS zircon geochronology, where analytical precision is high and confounding open system behaviour is relatively well controlled. Here, a plethora of competing age interpretations have developed in the literature, falling into three broad categories (e.g., Samperton et al., 2015Samperton, K.M., Schoene, B., Cottle, J.M., Keller, C.B., Crowley, J.L., Schmitz, M.D. (2015) Magma emplacement, differentiation and cooling in the middle crust: Integrated zircon geochronological–geochemical constraints from the Bergell Intrusion, Central Alps. Chemical Geology 417, 322–340.
) shown in Fig. 1f.(1) Weighted mean. In cases where the variance of the dataset is plausibly consistent with analytical uncertainty alone, then some authors may calculate a weighted mean of the entire dataset (e.g., Crowley et al., 2007
Crowley, J.L., Schoene, B., Bowring, S.A. (2007) U-Pb dating of zircon in the Bishop Tuff at the millennial scale. Geology 35, 1123–1126.
).(2) Youngest zircon. In contrast, where there is an expectation of slow crystallisation relative to analytical uncertainty, or ages are highly dispersed, the youngest single analysis may be considered a better estimate of eruption age (e.g., Wotzlaw et al., 2013
Wotzlaw, J.F., Schaltegger, U., Frick, D.A., Dungan, M.A., Gerdes, A., Günther, D. (2013) Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41, 867–870.
).(3) Low MSWD weighted mean. As an intermediate between (1) and (2), one may calculate a weighted mean of only the N youngest analyses such that, given the acceptance distribution of the MSWD (Wendt and Carl, 1991
Wendt, I., Carl, C. (1991) The statistical distribution of the mean squared weighted deviation. Chemical Geology 86, 275–285.
), the MSWD of this subpopulation does not exceed a value deemed acceptable for N analyses (e.g., Schoene et al., 2015Schoene, B., Samperton, K.M., Eddy, M.P., Keller, G., Adatte, T., Bowring, S.A., Khadri, S.F.R., Gertsch, B. (2015) U-Pb geochronology of the Deccan Traps and relation to the end-Cretaceous mass extinction. Science 347, 182–184.
).The possibility for residual lead loss, even following chemical abrasion, substantially complicates each of these three approaches, as does the common practice of excluding outliers subjectively identified as antecrysts. While interpretation (1) is likely to systematically pre-date the true eruption age, the accuracy of (2) and (3) has not been well tested. Moreover, while each interpretation has advantages, it is not clear that any of the three yields a statistically robust estimate of eruption age.
top
Model Configuration
In order to address these problems, we investigate the performance of common weighted-mean, youngest-zircon, and MSWD-test age interpretations, as well as that of an alternative likelihood-based Bayesian approach. To this end, we consider two dimensionless variables which, together with the pre-eruptive zircon crystallisation distribution f(tr), determine the behaviour of all possible volcanic zircon age interpretations. The first is ∆t/σ, the ratio of the true crystallisation timescale ∆t to analytical uncertainty σ, while the second is simply N, the number of analyses (Fig. 1).
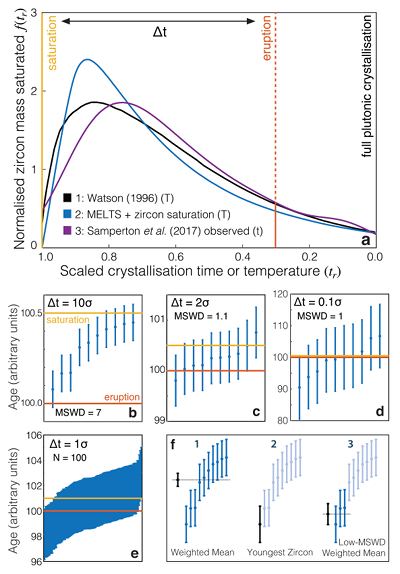
Figure 1 Zircon distributions. (a) Theoretical and empirical relative zircon crystallisation distributions f(tr), scaled from initiation to termination of zircon crystallisation. 1: Kinetic model of Watson (1996)
Watson, E.B. (1996) Dissolution, growth and survival of zircons during crustal fusion: kinetic principles, geological models and implications for isotopic inheritance. Transactions of the Royal Society of Edinburgh: Earth Sciences 87, 43–56.
, based on zirconium diffusion constraints. 2: Thermodynamic model of Keller et al. (2017)Keller, C.B., Boehnke, P., Schoene, B. (2017) Temporal variation in relative zircon abundance throughout Earth history. Geochemical Perspectives Letters 3, 179–189.
using MELTS calculations. 3: Observed zircon crystallisation distributions of Samperton et al. (2017)Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
, shown as a kernel density estimate for all autocrystic zircons, truncated at +/- 1 kernel bandwidth. (b-d) Representative synthetic zircon age datasets for a variety of ∆t/σ at N = 10. (e) Example dataset with N = 100 at ∆t = 1σ; note the range is greater than in c despite lower ∆t. (f) Schematic illustration of the three most common volcanic zircon age interpretations.For instantaneous crystallisation (∆t/σ = 0) with Gaussian analytical uncertainty, both the mean and variance of an analytical dataset are constant as a function of N, and a weighted-mean interpretation is fully justified. However, these assumptions fail for non-trivial ∆t, leading to systematic bias and potentially major over-estimation of accuracy and precision at high N. In contrast, at high ∆t/σ, a youngest-zircon estimate is likely to outperform a weighted-mean interpretation, but may systematically pre- or post-date the true eruption age as a function of N.
The effectiveness of each approach will depend on f(tr). Fortunately, magmatic zircon crystallisation behaviour is understood via empirical saturation equations (Boehnke et al., 2013
Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
), kinetic models (Watson, 1996Watson, E.B. (1996) Dissolution, growth and survival of zircons during crustal fusion: kinetic principles, geological models and implications for isotopic inheritance. Transactions of the Royal Society of Edinburgh: Earth Sciences 87, 43–56.
), and observation of natural systems (e.g., Samperton et al., 2017Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
). In particular, we consider the mass of zircon crystallised per unit time or temperature per unit mass of magma. This intensive distribution should not be confused with the zircon populations considered by Caricchi et al. (2014Caricchi, L., Simpson, G., Schaltegger, U. (2014) Zircons reveal magma fluxes in the Earth’s crust. Nature 511, 457–461.
, 2016Caricchi, L., Simp son, G., Schaltegger, U. (2016) Estimates of volume and magma input in crustal magmatic systems from zircon geochronology: the effect of modelling assumptions and system variables. Frontiers in Earth Science 4, 1–15.
), who assume constant zircon crystallisation rate per unit magma in the saturation interval (i.e. a flat line in Fig. 1a) in their attempt to estimate pluton-scale magma fluxes, which we do not consider here.Watson (1996)
Watson, E.B. (1996) Dissolution, growth and survival of zircons during crustal fusion: kinetic principles, geological models and implications for isotopic inheritance. Transactions of the Royal Society of Edinburgh: Earth Sciences 87, 43–56.
was the first to consider the form of the relative zircon crystallisation distribution as a function of temperature, calculating a theoretical distribution on the basis of kinetic constraints, characterised by a rapid onset of zircon crystallisation followed by a gradual decline. We also consider a thermodynamic model integrating major and trace element evolution with empirical zircon saturation equations (Boehnke et al., 2013Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
; Keller et al., 2017Keller, C.B., Boehnke, P., Schoene, B. (2017) Temporal variation in relative zircon abundance throughout Earth history. Geochemical Perspectives Letters 3, 179–189.
), as well as an observed average plutonic zircon distribution (as a function of time) derived from CA-ID-TIMS of both single zircons and sub-grain zircon fragments (Samperton et al., 2017Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
). All three approaches yield similar distributions, (Fig. 1a) – a consistency that extends in thermodynamic models to a wide range of whole rock compositions despite greatly varying saturation conditions (Fig. S-1). Distributions #1 and #2 assume linear cooling of a single magma batch; interaction of multiple magma batches and variable cooling rates may distort the distribution, though an abrupt truncation at eruption must feature in all volcanic zircon age spectra.Given such a prior expectation of the form of f(tr), we may quantitatively test the performance of each common age interpretation as a function of N and ∆t/σ by drawing N zircons from a crystallisation distribution with arbitrary saturation and eruption ages, adding analytical uncertainty as a Gaussian random variable with variance σ2 relative to the ∆t of the distribution, applying each age interpretation to the resulting synthetic dataset, and repeating the process very many times for each N and ∆t/σ of interest. However, due to the consistency of theoretical and empirical zircon crystallisation distributions, we may also use such a distribution as prior information to constrain a likelihood-based Bayesian eruption age estimator as follows. Given an observed dataset and an accurate f(tr), one may readily calculate the likelihood of obtaining the observed dataset from the crystallisation distribution for any given saturation time and eruption time.
While a maximum-likelihood solution might be found by systematically varying both the saturation and eruption age to produce a two dimensional likelihood surface (e.g., Fig. S-2), such an exhaustive search would be inefficient. Instead, we follow the Metropolis algorithm to estimate the distribution of the eruption age, exploring the likelihood space by moving from its current position to a proposed position in the likelihood space with probability equal to the ratio of proposed and current likelihoods (maximum 1), with each proposal deviating from the previous position in only one dimension at a time (Gelman et al., 2013
Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., Rubin, D.B. (2013) Bayesian Data Analysis. CRC Press.
). After an initial period of equilibration, the series of accepted proposals takes the form of the stationary distribution of a Markov chain (Fig. S-3), which provides both the mean and variance of estimated zircon saturation and eruption ages. In order to test the sensitivity of this approach to the choice of f(tr), we calculate Bayesian eruption age estimates using (1) the MELTS crystallisation distribution (Fig. 1a) from which the synthetic data were drawn, (2) a uniform relative crystallisation distribution (i.e. a flat line in Fig. 1a), and (3) a “bootstrapped” distribution, a truncated kernel density estimate of each synthetic dataset (Methods).top
Results
We explore the parameter space from ∆t/σ of 0.01 to 10 and N of 1 to 1000, which includes ranges applicable to both ID-TIMS and in situ geochronological techniques. As expected, weighted means are accurate at very low ∆t/σ, with the lowest absolute error and accurate reported uncertainty at ∆t = 0.01σ (Fig. 2a,e), but fail at high ∆t/σ, with absolute error not lower than ∆t/2 and highly inaccurate reported uncertainty (Fig. 2d,h). Conversely, the youngest-zircon approach performs poorly at ∆t = 0.01σ with high absolute error and substantial over-precision, but comparatively well at ∆t = 10σ. Such interpretations might remain useful if ∆t/σ were readily determinable for natural datasets.
Problems emerge at intermediate levels of age dispersion. At ∆t = 1σ, all three traditional interpretations begin to fail visibly above N = 3, with high absolute error in youngest-zircon interpretations, and under-estimated uncertainty in both weighted-mean and low-MSWD weighted-mean interpretations, for instance by a factor of two at N = 10 (Fig. 2b,f). At ∆t = 2σ, the problems with weighted-mean interpretations are accentuated, while youngest-zircon interpretations coincidentally perform well at moderate N (due to competing biases which happen to cancel at N = 5 and ∆t = 2σ), but ultimately still fail at high N due to analytical outliers.
These problems are compounded by the fact that the average MSWD at ∆t = 2σ is only 1.26, statistically indistinguishable from the near-unity MSWD of a dataset with ∆t = 0.01 σ until one has characterised more than ∼700 individual zircon analyses (Fig. S-4). Even magmatic age heterogeneity as high as ∆t = 5σ is not clearly distinguishable from instantaneous crystallisation on the basis of MSWD for datasets smaller than N ≈ 50, and data sets with ∆t/σ less than two are generally indistinguishable from instantaneous crystallisation at any practical N (Fig. S-4).
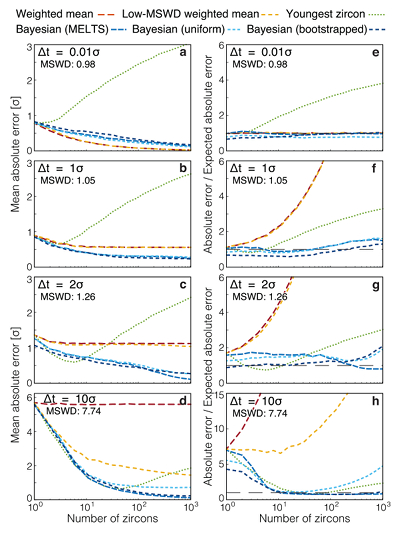
Figure 2 Performance of each age interpretation as a function of N and ∆t/σ. (a-d) Mean absolute error is the mean absolute deviation of the model result from the true value; lower absolute errors are better. (e-h) Accuracy of the model uncertainty for each age interpretation. A value greater than 1.0 indicates an under-estimation of the model uncertainty (i.e. over-precision), while a value lower than 1.0 indicates an over-estimation of the model uncertainty. MSWD in each panel is the average mean square of weighted deviation (also known as the reduced chi squared statistic) for that ∆t/σ over all N. Each datum reflects the mean of 1200 synthetic dataset tests; standard error of the mean is on the order of the line width.
In contrast, the Bayesian eruption age estimate yields slightly higher absolute error than the weighted mean at ∆t = 0.01σ, but otherwise equals or outperforms all other approaches across a wide range of N and ∆t/σ, with the closest to consistently accurate reported uncertainties. Notably, this result is not highly sensitive to the exact choice of f(tr), as the Bayesian estimate assuming a uniform f(tr) only diverges from the equivalent estimate assuming the true prior at high ∆t/σ, and only then for N greater than typical in TIMS studies (ca. 5-20).
To explore the practical application of Bayesian eruption age estimation, we consider ID-TIMS datasets from two well-known super-eruptions with contrasting zircon age spectra: the 28 Ma Fish Canyon Tuff, with ∼500 kyr of continuous zircon age dispersion (Wotzlaw et al., 2013
Wotzlaw, J.F., Schaltegger, U., Frick, D.A., Dungan, M.A., Gerdes, A., Günther, D. (2013) Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41, 867–870.
), and the more homogeneous 767 kyr Bishop Tuff (Crowley et al., 2007Crowley, J.L., Schoene, B., Bowring, S.A. (2007) U-Pb dating of zircon in the Bishop Tuff at the millennial scale. Geology 35, 1123–1126.
). As seen in Figure 3, the results are suggestive of a youngest-zircon interpretation for the Fish Canyon Tuff and a weighted-mean interpretation for the Bishop Tuff – congruous with the dramatic difference in dispersion between the two datasets. If all zircons were strictly autocrystic, the presence of older outliers would suggest that we are incompletely sampling the zircon saturation distribution, and thus over-estimating the eruption age. Including xenocrystic outliers in the Bayesian age interpretation thus counter-intuitively leads to under-estimation of the eruption age and divergence between Bayesian and weighted-mean ages for the Bishop Tuff (e.g., Fig. S-5).
Figure 3 Bayesian eruption age estimates for two well known volcanic zircon populations. For age spectra with well-resolved dispersion (a), a kernel density estimate may recover a close approximation of f(tr), obviating the need to identify and reject antecrysts. However, for age spectra where igneous dispersion is not well resolved (b), assuming a uniform f(tr) may be more parsimonious.
top
Discussion
Considering the results of Figure 2 in context of the variance of the MSWD (Fig. S-4), for most natural datasets we cannot rely on sufficiently low ∆t/σ to justify a weighted-mean interpretation even at low MSWD, nor in general can we justify a youngest-zircon interpretation except at low N and high MSWD. In the absence of reliable external evidence for instantaneous crystallisation, the greater precision obtained by a weighted-mean approach is illusory. A likelihood-based Bayesian estimate appears to perform competitively under all scenarios, and is the least likely to underestimate the reported uncertainty.
The problem of minimum age estimation may also be considered from the perspective of mixture modelling, which can be approached either numerically or analytically (Galbraith, 2005
Galbraith, R. (2005) Statistics for Fission Track Analysis. CRC Press.
; Jasra et al., 2006Harrison, T.M. (2009) The Hadean Crust: Evidence from 4 Ga Zircons. Annual Review of Earth and Planetary Sciences 37, 479–505.
), and is also likely to outperform the “traditional” interpretations. In this context, the main advantage of our approach compared to an analytical equivalent is merely the ability to specify numerically an arbitrary f(tr) derived from a physics-based model.While our approach may decrease the impact of subjective interpretational decisions, it does not eliminate them entirely: we must still choose a method by which to estimate f(tr). This relative crystallisation distribution is well-determined for a single magma batch (Fig. 1a #1-2), and may be empirically estimated (“bootstrapped”) by a kernel density estimate in datasets with highly- resolved dispersion (Fig. 1a #3). Even when data are inverted with an f(tr) that does not match the distribution from which they were drawn, a Bayesian approach still significantly outperforms traditional interpretations (Fig. 2, Figs. S-6, S-7). Nonetheless, distortions may occur, particularly in datasets featuring extreme outliers, or if our critical assumption that f(tr) falls to zero at tr = 0 (i.e. no crystallisation after eruption) is violated by contamination, unrecognised lead loss, or other open system behaviour.
Finally, while the similarity in form between the observed and theoretical relative crystallisation distributions f(tr) (Fig. 1a) suggests that single zircon and zircon fragment TIMS ages are sampling (and not simply integrating) the true f(tr), further systematic analysis is required. The ideal U-Pb zircon technique to resolve such geochronological problems must provide high analytical accuracy, high spatial resolution, and the ability to mitigate lead loss. Consequently, we recommend sub-grain microsampling or microfracturing wherever possible in TIMS analyses (e.g., Samperton et al., 2017
Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
), and emphasise further study of the effects and detection of lead loss for all U-Pb techniques.top
Acknowledgements
Thanks to B. Dyer and J.-F. Wotzlaw for discussion and to P. Vermeesch, K. Gallagher, U. Schaltegger, and T. Sheldrake for valuable reviews. CBK. was supported in part by the Department of Energy Computational Science Graduate Fellowship Program of the Office of Science and National Nuclear Security Administration under contract DE- FG02-97ER25308. Computational support was provided by the Princeton Institute for Computational Science and Engineering. Lawrence Livermore National Laboratory is operated by Lawrence Livermore National Security, LLC, for the U.S. Department of Energy, National Nuclear Security Administration under Contract DE-AC52-07NA27344. All source code is available at https://github.com/brenhinkeller/BayeZirChron.c
top
References
Boehnke, P., Watson, E.B., Trail, D., Harrison, T.M., Schmitt, A.K. (2013) Zircon saturation re-revisited. Chemical Geology 351, 324–334.
 Show in context
Show in context Moreover, even though zircon saturation in magmas is empirically well understood and distinct from whole rock crystallisation to the solidus (Boehnke et al., 2013), U-Pb zircon ages are traditionally interpreted within uncertainty as reflecting bulk crystallisation or eruption.
View in article
Fortunately, magmatic zircon crystallisation behaviour is understood via empirical saturation equations (Boehnke et al., 2013), kinetic models (Watson, 1996), and observation of natural systems (e.g., Samperton et al., 2017).
View in article
We also consider a thermodynamic model integrating major and trace element evolution with empirical zircon saturation equations (Boehnke et al., 2013; Keller et al., 2017), as well as an observed average plutonic zircon distribution (as a function of time) derived from CA-ID-TIMS of both single zircons and sub-grain zircon fragments (Samperton et al., 2017).
View in article
Bowring, S.A., Grotzinger, J.P., Isachsen, C., Knoll, A., Pelechaty, S., Kolosov, P. (1993) Calibrating rates of early Cambrian evolution. Science 261, 1293–1298.
 Show in context
Show in context Throughout the geologic record, zircon provides crucial time constraints for processes ranging from evolution and mass extinction to magmatism and crustal differentiation (Bowring et al., 1993; Mundil et al., 2004; Harrison, 2009; Schoene et al., 2015; Samperton et al., 2017).
View in article
However, the crystallisation of a suite of zircons in a single igneous rock sample has often been assumed to occur rapidly relative to analytical uncertainty, justifying the use of statistical approaches such as the weighted mean (e.g., Bowring et al., 1993).
View in article
Caricchi, L., Simpson, G., Schaltegger, U. (2014) Zircons reveal magma fluxes in the Earth’s crust. Nature 511, 457–461.
 Show in context
Show in contextThis intensive distribution should not be confused with the zircon populations considered by Caricchi et al. (2014, 2016), who assume constant zircon crystallisation rate per unit magma in the saturation interval (i.e. a flat line in Fig. 1a) in their attempt to estimate pluton-scale magma fluxes, which we do not consider here.
View in article
Caricchi, L., Simp son, G., Schaltegger, U. (2016) Estimates of volume and magma input in crustal magmatic systems from zircon geochronology: the effect of modelling assumptions and system variables. Frontiers in Earth Science 4, 1–15.
 Show in context
Show in contextThis intensive distribution should not be confused with the zircon populations considered by Caricchi et al. (2014, 2016), who assume constant zircon crystallisation rate per unit magma in the saturation interval (i.e. a flat line in Fig. 1a) in their attempt to estimate pluton-scale magma fluxes, which we do not consider here.
View in article
Cherniak, D.J. (2003) Diffusion in Zircon. Reviews in Mineralogy and Geochemistry 53, 113–143.
 Show in context
Show in context Due to extremely slow parent and daughter isotope diffusion (Cherniak, 2003), zircon U-Pb ages record zircon crystallisation, if not compromised by metamictisation and subsequent Pb loss.
View in article
Crowley, J.L., Schoene, B., Bowring, S.A. (2007) U-Pb dating of zircon in the Bishop Tuff at the millennial scale. Geology 35, 1123–1126.
 Show in context
Show in contextIn cases where the variance of the dataset is plausibly consistent with analytical uncertainty alone, then some authors may calculate a weighted mean of the entire dataset (e.g., Crowley et al., 2007).
View in article
To explore the practical application of Bayesian eruption age estimation, we consider ID-TIMS datasets from two well-known super-eruptions with contrasting zircon age spectra: the 28 Ma Fish Canyon Tuff, with ∼500 kyr of continuous zircon age dispersion (Wotzlaw et al., 2013), and the more homogeneous 767 kyr Bishop Tuff (Crowley et al., 2007).
View in article
Ellis, B.S., Mark, D.F., Troch, J., Bachmann, O., Guillong, M., Kent, A.J.R., von Quadt, A. (2017) Split-grain 40Ar/39Ar dating: Integrating temporal and geochemical data from crystal cargoes. Chemical Geology 457, 15–23.
 Show in context
Show in context Analogous issues appear in other geochronological applications ranging from the interpretation of anomalously dispersed Ar-Ar ages (e.g., Ellis et al., 2017) to the estimation of sedimentary depositional ages from detrital mineral geochronology.
View in article
Galbraith, R. (2005) Statistics for Fission Track Analysis. CRC Press.
 Show in context
Show in context The problem of minimum age estimation may also be considered from the perspective of mixture modelling, which can be approached either numerically or analytically (Galbraith, 2005; Jasra et al., 2006), and is also likely to outperform the “traditional” interpretations.
View in article
Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., Rubin, D.B. (2013) Bayesian Data Analysis. CRC Press.
 Show in context
Show in contextInstead, we follow the Metropolis algorithm to estimate the distribution of the eruption age, exploring the likelihood space by moving from its current position to a proposed position in the likelihood space with probability equal to the ratio of proposed and current likelihoods (maximum 1), with each proposal deviating from the previous position in only one dimension at a time (Gelman et al., 2013).
View in article
Harrison, T.M. (2009) The Hadean Crust: Evidence from 4 Ga Zircons. Annual Review of Earth and Planetary Sciences 37, 479–505.
 Show in context
Show in context Throughout the geologic record, zircon provides crucial time constraints for processes ranging from evolution and mass extinction to magmatism and crustal differentiation (Bowring et al., 1993; Mundil et al., 2004; Harrison, 2009; Schoene et al., 2015; Samperton et al., 2017).
View in article
Jasra, A., Stephens, D.A., Gallagher, K., Holmes, C.C. (2006) Bayesian Mixture Modelling in Geochronology via Markov Chain Monte Carlo. Mathematical Geology 38, 269–300.
 Show in context
Show in context The problem of minimum age estimation may also be considered from the perspective of mixture modelling, which can be approached either numerically or analytically (Galbraith, 2005; Jasra et al., 2006), and is also likely to outperform the “traditional” interpretations.
View in article
Keller, C.B., Boehnke, P., Schoene, B. (2017) Temporal variation in relative zircon abundance throughout Earth history. Geochemical Perspectives Letters 3, 179–189.
 Show in context
Show in context Figure 1 [...] Thermodynamic model of Keller et al. (2017) using MELTS calculations.
View in article
We also consider a thermodynamic model integrating major and trace element evolution with empirical zircon saturation equations (Boehnke et al., 2013; Keller et al., 2017), as well as an observed average plutonic zircon distribution (as a function of time) derived from CA-ID-TIMS of both single zircons and sub-grain zircon fragments (Samperton et al., 2017).
View in article
Lissenberg, C.J., Rioux, M., Shimizu, N., Bowring, S.A., Mével, C. (2009) Zircon Dating of Oceanic Crustal Accretion. Science 323, 1048–1050.
 Show in context
Show in context While such assumptions may be justified for sufficiently ancient or homogeneous samples, crystallisation timescales may span 200-700 kyr for magmatic zircons (Lissenberg et al., 2009; Wotzlaw et al., 2013; Samperton et al., 2017).
View in article
Mattinson, J.M. (2005) Zircon U–Pb chemical abrasion (“CA-TIMS”) method: Combined annealing and multi-step partial dissolution analysis for improved precision and accuracy of zircon ages. Chemical Geology 220, 47–66.
 Show in context
Show in context For instance, modern U-Pb Chemical Abrasion – Isotope Dilution TIMS (CA-ID-TIMS) ages (Mattinson, 2005) on single zircons and zircon fragments may surpass 0.05 % (2σ) accuracy and precision (e.g., Schoene et al., 2015; Samperton et al., 2017) – equivalent to 50 kyr in a 100 Ma sample.
View in article
Mundil, R., Ludwig, K.R., Metcalfe, I., Renne, P.R. (2004) Age and Timing of the Permian Mass Extinctions: U/Pb Dating of Closed-System Zircons. Science 305, 1760–1763.
 Show in context
Show in contextThroughout the geologic record, zircon provides crucial time constraints for processes ranging from evolution and mass extinction to magmatism and crustal differentiation (Bowring et al., 1993; Mundil et al., 2004; Harrison, 2009; Schoene et al., 2015; Samperton et al., 2017).
View in article
Reiners, P.W., Carlson, R.W., Renne, P.R., Cooper, K.M., Granger, D.E., McLean, N.M., Schoene, B. (2018) Geochronology and Thermochronology. John Wiley & Sons.
 Show in context
Show in context Absolute time constraints are critical for establishing temporal correlations, testing casual relationships, and quantifying rates and durations throughout the Earth sciences (Reiners et al., 2018).
View in article
Samperton, K.M., Schoene, B., Cottle, J.M., Keller, C.B., Crowley, J.L., Schmitz, M.D. (2015) Magma emplacement, differentiation and cooling in the middle crust: Integrated zircon geochronological–geochemical constraints from the Bergell Intrusion, Central Alps. Chemical Geology 417, 322–340.
 Show in context
Show in context Here, a plethora of competing age interpretations have developed in the literature, falling into three broad categories (e.g., Samperton et al., 2015) shown in Fig. 1f.
View in article
Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
 Show in context
Show in context Throughout the geologic record, zircon provides crucial time constraints for processes ranging from evolution and mass extinction to magmatism and crustal differentiation (Bowring et al., 1993; Mundil et al., 2004; Harrison, 2009; Schoene et al., 2015; Samperton et al., 2017).
View in article
While such assumptions may be justified for sufficiently ancient or homogeneous samples, crystallisation timescales may span 200-700 kyr for magmatic zircons (Lissenberg et al., 2009; Wotzlaw et al., 2013; Samperton et al., 2017).
View in article
For instance, modern U-Pb Chemical Abrasion – Isotope Dilution TIMS (CA-ID-TIMS) ages (Mattinson, 2005) on single zircons and zircon fragments may surpass 0.05 % (2σ) accuracy and precision (e.g., Schoene et al., 2015; Samperton et al., 2017) – equivalent to 50 kyr in a 100 Ma sample.
View in article
Consequently, zircon crystallisation age heterogeneity is increasingly clearly resolved in a wide range of magmatic contexts (Wotzlaw et al., 2013; Samperton et al., 2017).
View in article
Figure 1 [...] Observed zircon crystallisation distributions of Samperton et al. (2017), shown as a kernel density estimate for all autocrystic zircons, truncated at +/- 1 kernel bandwidth.
View in article
Fortunately, magmatic zircon crystallisation behaviour is understood via empirical saturation equations (Boehnke et al., 2013), kinetic models (Watson, 1996), and observation of natural systems (e.g., Samperton et al., 2017).
View in article
We also consider a thermodynamic model integrating major and trace element evolution with empirical zircon saturation equations (Boehnke et al., 2013; Keller et al., 2017), as well as an observed average plutonic zircon distribution (as a function of time) derived from CA-ID-TIMS of both single zircons and sub-grain zircon fragments (Samperton et al., 2017).
View in article
Consequently, we recommend sub-grain microsampling or microfracturing wherever possible in TIMS analyses (e.g., Samperton et al., 2017), and emphasise further study of the effects and detection of lead loss for all U-Pb techniques.
View in article
Schoene, B. (2014) 4.10 U–Th–Pb Geochronology. In: Rudnick, R.L. (Ed.) Treatise on Geochemistry, Second Edition. Elsevier, 341–378.
 Show in context
Show in context Recently, however, continual improvements in analytical precision and accuracy have fundamentally altered longstanding assumptions of geochronological age interpretation (Schoene, 2014).
View in article
Schoene, B., Samperton, K.M., Eddy, M.P., Keller, G., Adatte, T., Bowring, S.A., Khadri, S.F.R., Gertsch, B. (2015) U-Pb geochronology of the Deccan Traps and relation to the end-Cretaceous mass extinction. Science 347, 182–184.
 Show in context
Show in context Throughout the geologic record, zircon provides crucial time constraints for processes ranging from evolution and mass extinction to magmatism and crustal differentiation (Bowring et al., 1993; Mundil et al., 2004; Harrison, 2009; Schoene et al., 2015; Samperton et al., 2017).
View in article
For instance, modern U-Pb Chemical Abrasion – Isotope Dilution TIMS (CA-ID-TIMS) ages (Mattinson, 2005) on single zircons and zircon fragments may surpass 0.05 % (2σ) accuracy and precision (e.g., Schoene et al., 2015; Samperton et al., 2017) – equivalent to 50 kyr in a 100 Ma sample.
View in article
As an intermediate between (1) and (2), one may calculate a weighted mean of only the N youngest analyses such that, given the acceptance distribution of the MSWD (Wendt and Carl, 1991), the MSWD of this subpopulation does not exceed a value deemed acceptable for N analyses (e.g., Schoene et al., 2015).
View in article
Watson, E.B. (1996) Dissolution, growth and survival of zircons during crustal fusion: kinetic principles, geological models and implications for isotopic inheritance. Transactions of the Royal Society of Edinburgh: Earth Sciences 87, 43–56.
 Show in context
Show in context Figure 1 [...] Kinetic model of Watson (1996), based on zirconium diffusion constraints
View in article
Fortunately, magmatic zircon crystallisation behaviour is understood via empirical saturation equations (Boehnke et al., 2013), kinetic models (Watson, 1996), and observation of natural systems (e.g., Samperton et al., 2017).
View in article
Watson (1996) was the first to consider the form of the relative zircon crystallisation distribution as a function of temperature, calculating a theoretical distribution on the basis of kinetic constraints, characterised by a rapid onset of zircon crystallisation followed by a gradual decline.
View in article
Wendt, I., Carl, C. (1991) The statistical distribution of the mean squared weighted deviation. Chemical Geology 86, 275–285.
 Show in context
Show in contextAs an intermediate between (1) and (2), one may calculate a weighted mean of only the N youngest analyses such that, given the acceptance distribution of the MSWD (Wendt and Carl, 1991), the MSWD of this subpopulation does not exceed a value deemed acceptable for N analyses (e.g., Schoene et al., 2015).
View in article
Wotzlaw, J.F., Schaltegger, U., Frick, D.A., Dungan, M.A., Gerdes, A., Günther, D. (2013) Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41, 867–870.
 Show in context
Show in contextWhile such assumptions may be justified for sufficiently ancient or homogeneous samples, crystallisation timescales may span 200-700 kyr for magmatic zircons (Lissenberg et al., 2009; Wotzlaw et al., 2013; Samperton et al., 2017).
View in article
Consequently, zircon crystallisation age heterogeneity is increasingly clearly resolved in a wide range of magmatic contexts (Wotzlaw et al., 2013; Samperton et al., 2017).
View in article
In contrast, where there is an expectation of slow crystallisation relative to analytical uncertainty, or ages are highly dispersed, the youngest single analysis may be considered a better estimate of eruption age (e.g., Wotzlaw et al., 2013).
View in article
To explore the practical application of Bayesian eruption age estimation, we consider ID-TIMS datasets from two well-known super-eruptions with contrasting zircon age spectra: the 28 Ma Fish Canyon Tuff, with ∼500 kyr of continuous zircon age dispersion (Wotzlaw et al., 2013), and the more homogeneous 767 kyr Bishop Tuff (Crowley et al., 2007).
View in article
top
Supplementary Information
The Supplementary Information includes:
- Supplementary Methods
- Figures S-1 to S-8
- Supplementary Information References
Download the Supplementary Information (PDF).
Figures and Tables
Figure 1 Zircon distributions. (a) Theoretical and empirical relative zircon crystallisation distributions f(tr), scaled from initiation to termination of zircon crystallisation. 1: Kinetic model of Watson (1996)
Watson, E.B. (1996) Dissolution, growth and survival of zircons during crustal fusion: kinetic principles, geological models and implications for isotopic inheritance. Transactions of the Royal Society of Edinburgh: Earth Sciences 87, 43–56.
, based on zirconium diffusion constraints. 2: Thermodynamic model of Keller et al. (2017)Keller, C.B., Boehnke, P., Schoene, B. (2017) Temporal variation in relative zircon abundance throughout Earth history. Geochemical Perspectives Letters 3, 179–189.
using MELTS calculations. 3: Observed zircon crystallisation distributions of Samperton et al. (2017)Samperton, K.M., Bell, E.A., Barboni, M., Keller, C.B., Schoene, B. (2017) Zircon age-temperature-compositional spectra in plutonic rocks. Geology 45, 983–986.
, shown as a kernel density estimate for all autocrystic zircons, truncated at +/- 1 kernel bandwidth. (b-d) Representative synthetic zircon age datasets for a variety of ∆t/σ at N = 10. (e) Example dataset with N = 100 at ∆t = 1σ; note the range is greater than in c despite lower ∆t. (f) Schematic illustration of the three most common volcanic zircon age interpretations.
Figure 2 Performance of each age interpretation as a function of N and ∆t/σ. (a-d) Mean absolute error is the mean absolute deviation of the model result from the true value; lower absolute errors are better. (e-h) Accuracy of the model uncertainty for each age interpretation. A value greater than 1.0 indicates an under-estimation of the model uncertainty (i.e. over-precision), while a value lower than 1.0 indicates an over-estimation of the model uncertainty. MSWD in each panel is the average mean square of weighted deviation (also known as the reduced chi squared statistic) for that ∆t/σ over all N. Each datum reflects the mean of 1200 synthetic dataset tests; standard error of the mean is on the order of the line width.
Figure 3 Bayesian eruption age estimates for two well known volcanic zircon populations. For age spectra with well-resolved dispersion (a), a kernel density estimate may recover a close approximation of f(tr), obviating the need to identify and reject antecrysts. However, for age spectra where igneous dispersion is not well resolved (b), assuming a uniform f(tr) may be more parsimonious.